Understanding Layer Normalization

Decoding its role, impact, and key differences in modern neural architectures

Photo by Ag PIC on Unsplash

In modern deep learning, layer normalization has emerged as a crucial technique for improving training stability and accelerating convergence. While its primary goal is to normalize inputs to reduce internal covariate shifts, the way LayerNorm interacts with architectures like Convolutional Neural Networks (CNNs) and Transformers differs significantly.

Purpose in Deep Learning

Layer normalization is a technique used in artificial neural networks to normalize the inputs to a given layer. Unlike batch normalization, which computes normalization statistics (mean and variance) across the batch dimension, layer normalization (LayerNorm) computes these statistics across the feature dimension for each individual input sample. This makes it especially useful for sequence models.

The process involves calculating the mean and variance of the features for a single input sample, then normalizing the features to have a mean of zero and a variance of one. After normalization, trainable parameters called gamma (for scaling) and beta (for shifting) can be applied, allowing the network to learn the optimal scale and offset for the normalized features. In both CNNs as well as Transformers, these params in the normalization layers are often omitted because subsequent layers can implitly learn those transformations.

This offers several benefits: It stabilizes training by reducing the sensitivity of the network to the scale of input features, leading to faster convergence and improved performance. One of the key challenges that LayerNorm addresses is internal covariate shift, a phenomenon where the distribution of inputs to a given layer changes during training as the model parameters are updated. This shift can slow down training, as the model constantly has to adapt to new input distributions. By normalizing the inputs across the features, LayerNorm reduces this shift, allowing each layer to learn more effectively and making the training process more stable. This is particularly useful in sequence-based models, where it enhances gradient flow and addresses challenges like exploding or vanishing gradients. Additionally, LayerNorm is resilient to variations in batch size, making it well-suited for tasks involving small or dynamic batches.

LayerNorm in a CNN vs. Transformer

LayerNorm behaves differently in Convolutional Neural Networks (CNNs) compared to Transformer architectures, such as in Transformer-based Large Language Models (LLMs) or Vision Transformers (ViTs). The difference lies in how the normalization is applied and what dimensions are normalized, leading to distinct implications for the respective architectures.

LayerNorm computed for a feature map in a CNN compared to LayerNorm computed for a token (or patch) in a Transformer

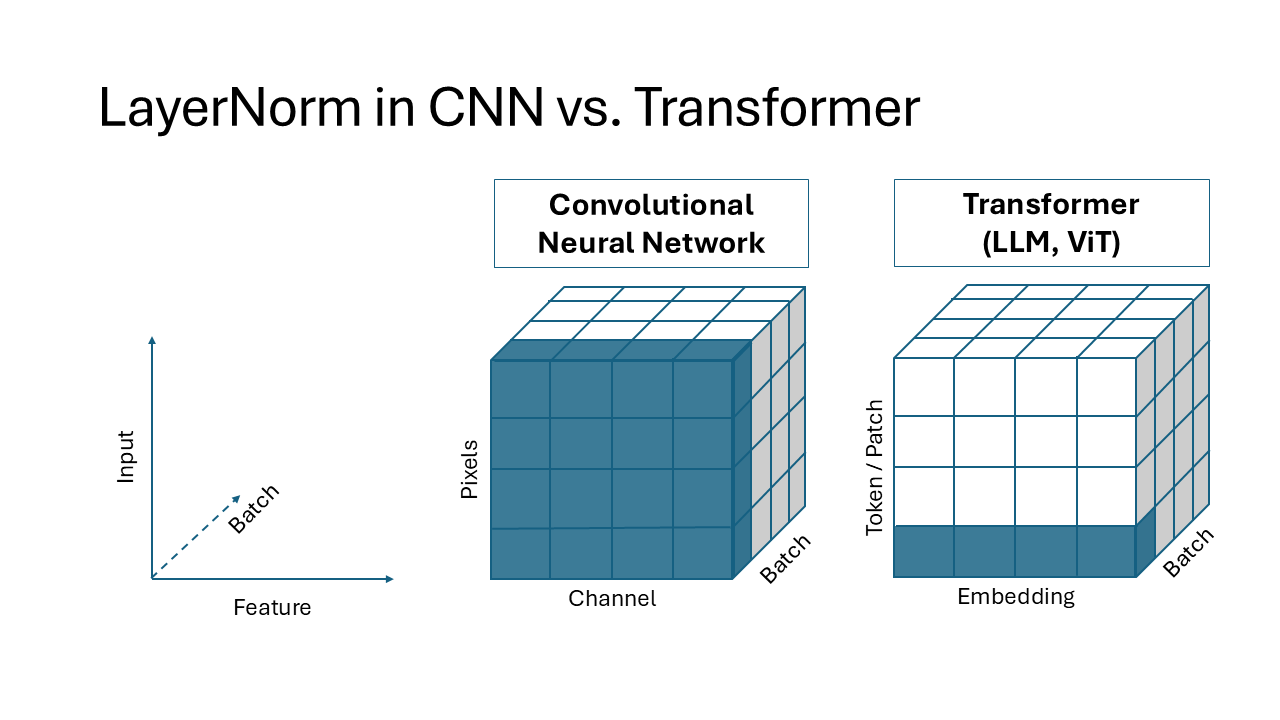
LayerNorm in CNNs

In CNNs, LayerNorm is typically applied to normalize the features at each spatial location independently. For a feature map, LayerNorm computes the mean and standard deviation across the channel dimension for each spatial location (height, width). This means:

• Each spatial position is treated as an independent entity.

• Normalization helps stabilizing the learning process by ensuring that the distribution of features at each spatial position remains consistent across channels.

\(y_{h, w, c} = \frac{x_{h, w, c} - \mu_{n, c}}{\sqrt{\sigma_{n, c}^2 + \epsilon}} * \gamma_c + \beta_c\)

LayerNorm in Transformers

In Transformer architectures, LayerNorm is applied differently: Transformers represent data as sequences of tokens (e.g., words), where each token has an embedding vector of size of the embedding dimensions. LayerNorm in this context computes the mean and standard deviation along the embedding dimensions for each token independently. This means:

- Each token is normalized independently of others in the sequence or image.

- Normalization ensures that the embedding of each token remains stable across layers, which is essential for effective attention calculations.

\(y_i = \frac{x_i - \mu_l}{\sqrt{\sigma_l^2 + \epsilon}} * \gamma_i + \beta_i\)

Implications for Computer Vision

This distinction how LayerNorm is computed in a CNN vs. Transformer architecture is particularly important in computer vision tasks, as normalization operates differently in a ViT compared to a CNN: In a ViT, an image is divided into patches, and each patch is treated as a token. LayerNorm in this context normalizes the feature vector representing each patch independently, ensuring consistent patch representations across the embedding dimensions. This approach prioritizes patch-to-patch interactions via attention mechanisms, which are crucial for ViTs.

The difference in how normalization is applied reflects the fundamental architectural distinctions between ViTs and CNNs: ViTs focus on global relationships and patch independence, while CNNs emphasize local spatial relationships and hierarchical feature extraction.

Comparing with InstanceNorm in a CNN

LayerNorm and Instance Normalization (InstanceNorm) share conceptual similarities in their approach to normalizing features, but they differ significantly in the dimensions they operate on and the contexts in which they are applied.

InstanceNorm computed along the spatial dimensions (height and width of an image) in a CNN compared to LayerNorm computed for a token (or patch) along the feature dimension in a Transformer

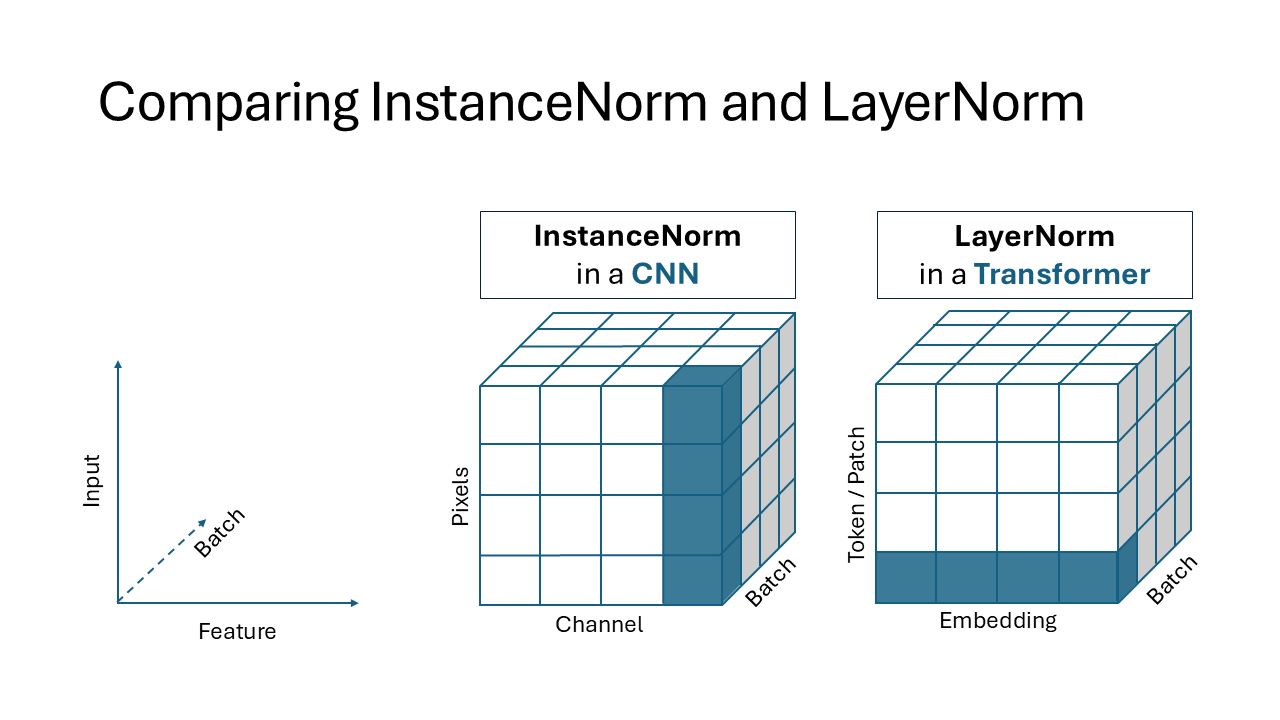
LayerNorm performs normalization across the embedding dimensions of each token independently. For example, in Transformers, each token is represented by a vector of features, and LayerNorm computes the mean and standard deviation for all the features within a single token (or patch). The normalization is then applied to the entire embedding vector of that token. This approach ensures consistency and stability in the token representations, enabling efficient attention-based computations. Conceptually, this resembles InstanceNorm, which normalizes features independently:

\(y_{h, w, c} = \frac{x_{h, w, c} - \mu_c}{\sqrt{\sigma_c^2 + \epsilon}} * \gamma_c + \beta_c\)

However, InstanceNorm operates across the spatial dimensions (e.g., height and width in an image), not across feature dimensions like LayerNorm.

Extending Layer Normalization Principle

The principles of normalization in Transformer architectures not only applies to LayerNorm but also extends to techniques like Root Mean Square Layer Normalization (RMSNorm):

\(y_i = \frac{x_i}{\sqrt{\frac{1}{n} \sum_{i=1}^{n} x_i^2 + \epsilon}} * \gamma_i\)

Both layer normalization methods share the goal of stabilizing token (or patch) representations by normalizing along embedding dimensions independently for each token . RMSNorm simplifies this process by normalizing using only the root mean square of the embeddings, rather than calculating both mean and variance, while still maintaining the independence of normalization across tokens. Unlike LayerNorm, RMSNorm omits the shift parameter (beta) as it inherently normalizes only the magnitude of the embeddings (via the root mean square), leaving the mean unaffected. Consequently, the shift parameter is unnecessary for preserving meaningful representations.

Therefore, like LayerNorm, RMSNorm enables Transformers to effectively manage varying token distributions within a sequence or across patches in an image.